11049 행렬 곱셈 순서
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같�
www.acmicpc.net
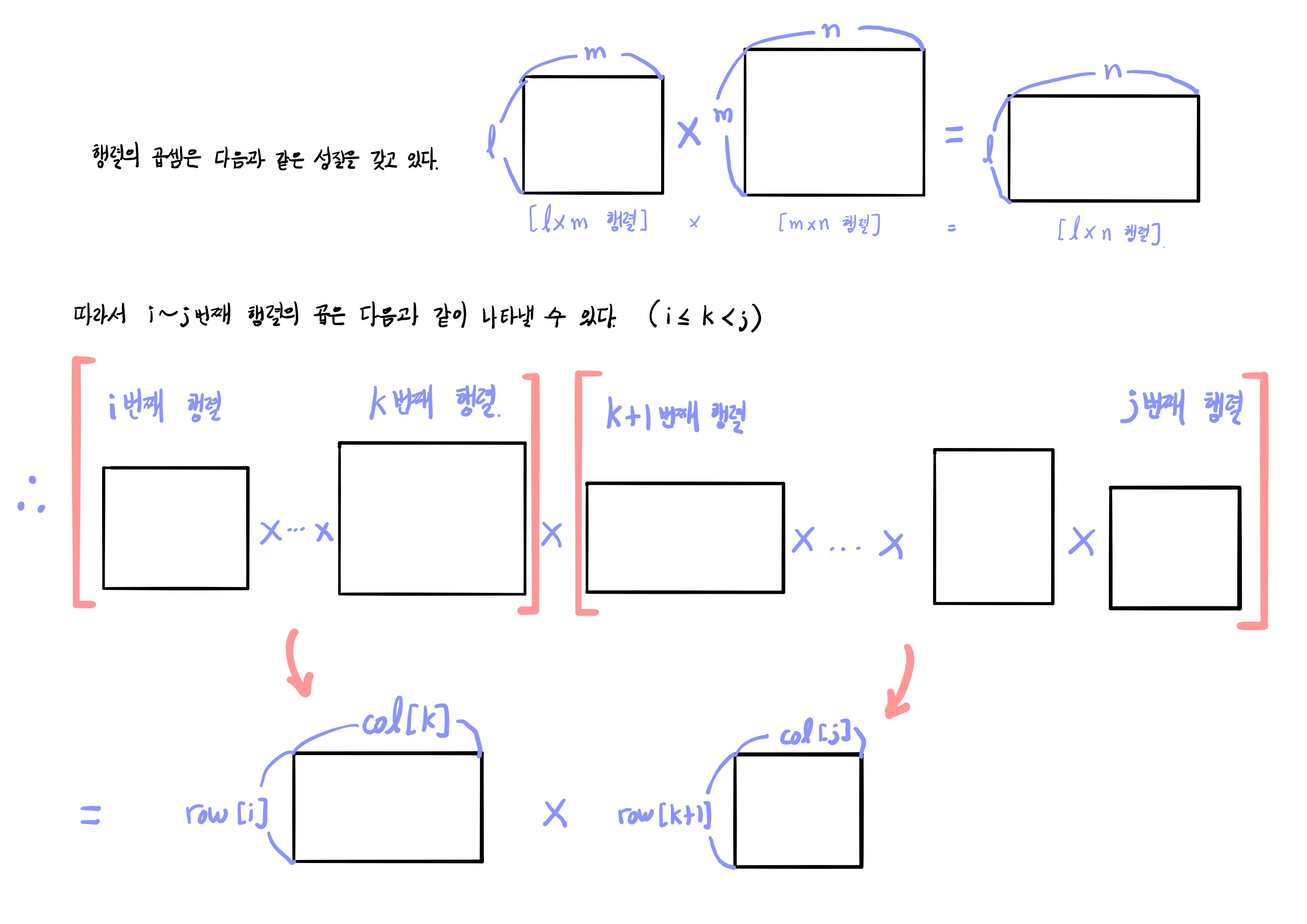
DP[i][j]를 구간 [i, j]에서의 최소 행렬 곱셈 회수라 하면,
DP[i][j] = k가 i부터 j까지 이동할 때 (DP[i][k] + DP[k+1][j] + row[i]*col[k]*col[j])의 최솟값이라 나타낼 수 있다.
i ~ j까지의 거리 (볼 행렬의 개수)를 먼저 고정하고, k를 움직여가며 i, j 각각에 대한 DP[i][j] 값을 구하는 방식으로 풀었다.
C++
#include <iostream>
#include <vector>
#include <algorithm>
#define INF 987654321
using namespace std;
typedef long long ll;
int row[503], col[503];
int DP[503][503];
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
int n, r, c;
cin >> n;
for(int i=0; i<n; i++) {
cin >> r >> c;
row[i] = r;
col[i] = c;
}
for(int len=1; len<n; len++){
for(int i=0; i<n; i++){
int j= i+len;
if(j >= n) break;
int res = INF;
for(int k=i; k<j; k++){
res = min(res, DP[i][k]+DP[k+1][j]+row[i]*col[k]*col[j]);
}
DP[i][j] = res;
}
}
cout << DP[0][n-1] << '\n';
return 0;
}
가장 바깥쪽 for문의 len은 볼 행렬의 개수, 두번째 for문의 i는 시작 행렬의 인덱스, 세번째 for문의 k는 곱셈 분기의 인덱스를 나타낸다.
'Algorithm > BOJ (백준)' 카테고리의 다른 글
| [C++] 백준 1699 제곱수의 합 (2) | 2020.07.25 |
|---|---|
| [C++] 백준 1149 RGB거리 (2) | 2020.07.25 |
| [C++] 백준 11053 가장 긴 증가하는 부분 순열 (2) | 2020.07.25 |
| [C++] 백준 9251 LCS (1) | 2020.07.24 |
| [C++] 백준 10974 모든 순열 (0) | 2020.07.24 |